Mínimo común múltiplo
En matemáticas, el mínimo común múltiplo (abreviado m.c.m), de dos o más números naturales es el menor número natural que es múltiplo de todos ellos. Sólo se aplica con números naturales, es decir, no se usan decimales, números negativos o números complejos.
Cálculo del mínimo común múltiplo (m.c.m)[editar]
Partiendo de 2 o más números y por descomposición en factores primos, expresados como producto de factores primos, su mínimo común múltiplo será el resultado de multiplicar los factores comunes y no comunes elevados a la mayor potencia, por ejemplo el mcm de 72 y 50 será:
|
|
|
Tomando los factores comunes y no comunes con su mayor exponente, tenemos que:
Conociendo el máximo común divisor de dos números, se puede calcular el mínimo común múltiplo de ellos, que será el producto de ambos dividido entre su máximo común divisor.
Propiedades básicas[editar]
- Si a es un entero, entonces [a, a] = a
- Cuando a y b son enteros, [a, b] = b si, sólo si b es múltiplo de a.
- (a,b) = [a,b] si son iguales u opuestos.
- [a, b] = [ab] si, sólo si (a,b)= 1
- [a/d, b/d] = [m/a, m/b] donde m = mcm y d = mcd. 1
- [ma,b]= m[a,b] si ([a,b]/a,m) = 1 2
- [a,b,c]= [[a,b], [b,c]]
- [a, b, c]|abc, donde abc ≠ 0
- [a,b,c] = abc (a,b,c)/(a,b)(b,c)(c,d)3
- Si el producto de dos números lo dividimos por su máximo común divisor dicho cociente es el mínimo común múltiplo.
- A y B que descompuestos en números primos será A=(p1·p2)·p3·p4 y B=(p1·p2)·p5·p6 donde si m.c.d. es (p1·p2) y el producto de A·B=(p1·p2)·p3·p4·(p1·p2)·p5·p6 donde vemos que (p1·p2) está repetido dos veces, luego si dividimos ese total por (p1·p2) tendremos el total menor que contiene a A y B siendo su mcm
- El mínimo común múltiplo de dos números, donde el menor divide al mayor, será el mayor. Es lógico ya que un múltiplo de ambos inferior al mayor sería imposible ya que no sería múltiplo del mayor.
- El mínimo común múltiplo de dos números primos es el total de su multiplicación. Esto es lógico ya que su máximo común divisor es 1.
- El mínimo común múltiplo de dos números compuestos será igual al cociente entre su producto y el m.c.d de ellos. Es evidente según la propiedad 1 de este tema.
- El máximo común divisor de varios números es un divisor del mínimo común múltiplo de tales números 4 .
- Sea mZ el conjunto de los múltiplos del entero m, nZ el del entero n. Entonces el conjunto nZ∩mZ está formado por los múltiplos comunes de m y n; en otra notación es el conjunto [m,n]Z. 5
Aplicaciones del mínimo común múltiplo[editar]
Suma de fracciones[editar]
Véase también: Mínimo común denominador
Véase también: Fracción
El mcm se puede emplear para sumar o restar fracciones de distinto denominador, tomando el mcm de los denominadores de las fracciones, y convirtiéndolas en fracciones equivalentes que puedan ser sumadas. Véase el siguiente ejemplo:
Para poder efectuar la suma, primero se debe buscar el mínimo común múltiplo de los denominadores (6 y 33)
|
|
|
luego el mínimo común múltiplo de 6 y 33 es:
que corresponde al número 66; ambas fracciones tendrán como denominador 66, ahora sólo hay que hallar a cada fracción su fracción equivalente, con denominador 66 y será posible la suma:
operando las fracciones, podemos realizar la suma:
Expresiones algebraicas[editar]
El m.c.m. para dos expresiones algebraicas, corresponde a la expresión algebraica de menor coeficiente numérico y de menor grado que es divisible exactamente por cada una de las expresiones dadas. Esta teoría es de suma importancia para las fracciones y ecuaciones.6

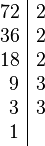
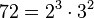
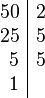

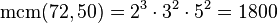
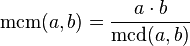


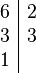






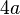 y
y  es
es  igualmente para
igualmente para  y
y  es
es 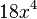 .
.
No hay comentarios.:
Publicar un comentario