Máximo común divisor
En matemáticas, se define el máximo común divisor (abreviado mcd o "M.C.D") de dos o más números enteros al mayor número que los divide sin dejar resto. Por ejemplo, el mcd de 42 y 56 es 14. En efecto:
operando:
Siendo 3 y 4 primos entre sí (no existe ningún número natural, aparte de 1, que divida a la vez al 3 y al 4).
Índice
[ocultar]Precisiones[editar]
Si a y b son números enteros distintos de cero y si el número c es de modo que c|a y a su vez c|b, a este número c se denomina divisor común de los números a y b.1 Obsérvese que dos números enteros cualesquiera tienen divisores comunes. Ellos son 1 y -1. Cuando existen, únicamente, como divisores comunes 1 y -1 de los números a y b, estos se llaman primos entre sí.
Un número entero d se llama máximo común divisor (mcd) de los números a y b cuando:
- d es divisor común de los números a y b y
- d es divisible por cualquier otro divisor común de los números a y b.
Como ejemplo, 12 es el mcd de 36 y 60. Pues 12|36 y 12|60; a su vez 12 es divisible por 1, -1, 2, -2, 4, -4, 6, -6, 12 y -12 que son divisores comunes de 36 y 60.2
Cálculo del MCD[editar]
Los dos métodos más utilizados para el cálculo del máximo común divisor de dos números son:
Por descomposición en factores primos[editar]
El máximo común divisor de dos números puede calcularse determinando la descomposición en factores primos de los dos números y tomando los factores comunes elevados a la menor potencia, el producto de los cuales será el mcd.
Ejemplo: para calcular el máximo común divisor de 48 y de 60 se obtiene de su factorización en factores primos.
|
|
|
El MCD son los factores comunes con su menor exponente, esto es:
En la práctica, este método solo es operativo para números pequeños tomando en general demasiado tiempo calcular la descomposición en factores primos de dos números cualquiera.
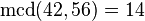




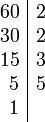
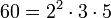
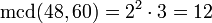
No hay comentarios.:
Publicar un comentario